A.5 Berechnungsmethoden

A.5.1 Verfahren nach NIEMEYER (1995)

Das gemäß den Auflagen zum Planfeststellungsbeschluss anzuwendende Verfahren zur Ermittlung der "ausbaubedingten Änderungen der mittleren Scheitelwasserstände", welches auch schon bei vorangegangenen Ausbaumaßnahmen sowohl an Unter- und Außenelbe (-13,5 m KN-Ausbau) als auch bei verschiedenen Vertiefungen der Unter- und Außenweser angewendet wurde, basiert auf einem Ansatz nach NIEMEYER (1995), der von folgendem theoretischen Konzept ausgeht:

Wenn die örtliche und zeitliche Variation der Wasserstände in dem Untersuchungsgebiet unmittelbar vor dem Eingriff durch eine oder mehrere vom Eingriff unabhängige Einflussgrößen funktional beschrieben werden kann, dann lassen sich mit Hilfe eben dieser Beziehung auch die fiktiven Wasserstände prognostizieren, die theoretisch ohne den Eingriff zu erwarten gewesen wären. Die Differenz dieser für den Prognosezeitraum nach dem Eingriff aus den unabhängigen Einflussgrößen berechneten hypothetischen Werte zu den tatsächlich beobachteten Wasserständen kann dann lt. NIEMEYER zur Quantifizierung der ausbaubedingten Wasserstandsänderungen herangezogen werden.

Um die Ergebnisse dieses Verfahrens in ihrer Aussagekraft richtig einordnen zu können, müssen zunächst die Voraussetzungen und Randbedingungen zur Anwendung des Verfahrens näher betrachtet werden, wobei im wissenschaftlichen Interesse auch eine kritische Beleuchtung der Grenzen des Verfahrens gestattet sein sollte, ohne damit die Anwendung des Verfahrens von vornherein ablehnen zu wollen.

Allgemeines Lineares Modell (ALM)

Als maßgebende Einflussgrößen zur Beschreibung der örtlichen Wasserstände an einem beliebigen Revierpegel (RP) im Ästuar mit den zuvor genannten Eigenschaften nennt Niemeyer den mittleren Tidenhub (MThb) und den mittleren Scheitelwasserstand (entsprechend der Fragestellung MTnw oder MThw) am Referenzpegel Helgoland sowie den von der Tide unbeeinflussten mittleren Oberwasserabfluss Q_m. Für das Elbeästuar sind hierbei die Abflussverhältnisse am Pegel Neu Darchau oberhalb des Wehres in Geesthacht zu Grunde zu legen.

Mit der Wahl dieser drei Einflussgrößen ist einerseits die Voraussetzung gegeben, dass die unabhängigen Variablen von einem Eingriff im Regime unbeeinflusst bleiben, andererseits werden aber auch die wesentlichen kausalen Wirkparameter zumindest implizit erfasst. Denn neben der direkten Berücksichtigung des Oberwasserabflusses, werden durch die Verwendung des Tidewasserstandes und des Tidenhubs am Pegel Helgoland, unweit des Mündungsgebietes der Elbe, auch die in diesen Parametern eingeprägten astronomisch und meteorologisch bedingten Variationen, die zweifellos in einem ursächlichen Zusammenhang mit der Variation des örtlichen Wasserstandes stehen, indirekt erfasst.

In dem von Niemeyer gewählten allgemeinen linearen Modell (ALM) wird die Zielgröße (der örtlich gesuchte Scheitelwasserstand MTnw bzw. MThw) am jeweiligen Revierpegel (RP) durch eine lineare Superposition der gewichteten unabhängigen Einflussgrößen dargestellt, wobei der Einfluss des Oberwasserabflusses in Neu Darchau, soweit er denn vorhanden ist, durch eine nichtlineare Gewichtung erfasst wird.

Für jeden zu betrachtenden Revierpegel (RP) im Ästuar müssen die Regressionskoeffizienten (a_RP) bis (e_RP) jeweils getrennt für die Tnw- bzw. Thw-Gleichung durch eine multiple Regressionsanalyse ermittelt werden. Im Rahmen dieser Untersuchungen wurde hierzu die Software CurveExpert2 © D. G. HYAMS 1995-1998 eingesetzt.

Von besonderer Bedeutung für die statistische Aussagekraft der gewonnenen Regressionskoeffizienten ist der Zeitraum über den die Regressionsanalyse zur Bestimmung der Regressionskoeffizienten (a_RP) bis (e_RP) durchgeführt wird. Abgesehen von der Notwendigkeit, dass dieser Zeitraum vor dem zu betrachtenden Eingriff gelegen haben muss, stellt die Anwendung stochastischer Methoden zur Beschreibung funktionaler Zusammenhänge gewisse Anforderungen an den Umfang und die Homogenität der Datenbasis. Nur wenn die Variationen der berücksichtigten Parameter in der zu erwartenden Bandbreite in der Datenbasis abgebildet sind, können auch die Ergebnisse als repräsentativ angesehen werden. Dabei sollte aus der Analyse jeder Stichprobe innerhalb der zur Verfügung stehenden Grundgesamtheit der Daten vergleichbare Ergebnisse resultieren.

NIEMEYER (1995) weist hinsichtlich der Festlegung des "unbeeinflussten" Bezugzeitraumes zudem darauf hin, dass die morphologischen Nachlaufwirkungen vorangegangener anthropogener Eingriffe abgeschlossen sein sollten, um das vorgeschlagene Modell sinnvoll anwenden zu können. Eine Differenzierung der aktuellen ausbaubedingten Änderungen von ggf. noch existenten morphologischen Nachlaufwirkungen zurückliegender anthropogener Eingriffe ist durch das gewählte Modell und den dabei berücksichtigten Parametern nicht abzubilden.

Die Anwendung des Verfahrens setzt somit voraus, dass sich die hydrologischen Verhältnisse im Ästuar vor dem Eingriff in einem stabilen Gleichgewichtszustand befunden haben müssen. Die Frage welche Folgen die Anwendung dieses Verfahrens auf instabile Verhältnisse bewirkt, wird später noch zu diskutieren sein.

Die Doppelsummenanalyse

Zur Festlegung solcher "unbeeinflusster" Zeiträume mit stabilen Verhältnissen wurde von NIEMEYER (1995) die sog. Doppelsummenanalyse nach WEISS & WILSON (1953); DYCK(1980) auf die Scheitelwasserstände angewendet, allerdings nur für die Revierpegel unterhalb Kollmars, da dieses Verfahren aufgrund der oberhalb von Kollmar einflussnehmenden Oberwasserwirkung nicht mehr anwendbar sei.

Bei der Doppelsummenanalyse werden die mittleren Scheitelwasserstände (bei NIEMEYER Jahresmittelwerte) am untersuchten Revierpegel sowie am Referenzpegel jeweils chronologisch aufaddiert und die nach jeder Addition resultierenden Summen zueinander in Relation gesetzt. Die so resultierenden Summenquotienten (Steigungen) können dann als Ganglinie über die Zeit auf getragen werden.

Verfahrensbedingt wird die Ganglinie der Quotienten mit fortschreitender Summation der in Relation gesetzten Parameter immer stärker geglättet, was damit zu erklären ist, dass es aufgrund der kontinuierlich zunehmenden Basis einer immer größeren Quotientenänderung bedarf um in Form eines signifikanten Ausschlags in Erscheinung zu treten.

Um diese im Grunde schleichende Quotientenänderung hervorzuheben, kann man eine sog. Unschärfe definieren, bis zu der eine geringfügige Änderung noch als akzeptierte Schwankung toleriert wird und der aktuelle Wert auf den letzten Wert zurückfällt. Erst bei Überscheiten dieser zugelassenen prozentualen Abweichung wird eine Änderung der Steigung als Sprung in der Ganglinie sichtbar.

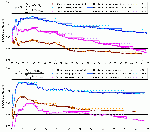
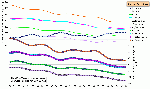
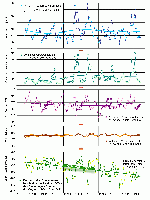
Damit hängt das Ergebnis dieser Methode nicht nur von der Länge des betrachteten Zeitraumes ab, sondern vielmehr auch von der individuellen Justierung der noch akzeptierten Unschärfe, die eine Steigungsänderung indiziert. Beispielhaft sind die Summenquotienten für das MTnw (hier Monatsmittelwerte) in Abb. A.5.1-1 an drei verschiedenen Revierpegel mit unterschiedlichen Unschärfen dargestellt.

Abb.A.5.1-1: Anwendung der Doppelsummenanalyse auf die Monatsmittelwerte der MTnw-Scheitel am Beispiel von drei verschiedenen Revierpegeln für unterschiedlich lange Zeiträume.

Der angesprochene Einfluss der Länge des Zeitraumes über den die Doppelsummenanalyse bis zu dem zu betrachtenden Zeitabschnitt bereits gelaufen ist, wird durch den unterschiedlichen Verlauf der Ganglinien im oberen Diagramm (Beginn der Aufsummierung 1978) und unteren Diagramm (Beginn der Aufsummierung 1991) deutlich erkennbar. Darüber hinaus zeichnet sich in Bezug auf die MTnw-Scheitel ein mehr oder weniger starker aber stetig fallender Trend über die Zeit ab, dessen Gradiente stromaufwärts zunimmt. Diese Tendenz ist auch bei den hier nicht dargestellten Pegelstandorten zu beobachten.

Allein das sich hier bereits abzeichnende Ergebnis eines sich stromaufwärts verstärkenden Trends, ist aus statistischer Sicht und unter Berücksichtigung der bereits erwähnten Einschränkungen und Voraussetzungen zur Anwendung des Modells weniger befriedigend. Lediglich für die Pegel unterhalb Glückstadts kann durch die Doppelsummenanalyse mit geringfügigen Abstrichen ein konstanter Bezugszeitraum ab Beginn der neunziger Jahre indiziert werden, wenn man den im oberen Diagramm gewählten längeren Zeitraum zu Grunde legt.

Damit die Festlegung des gesuchten unbeeinflussten Zeitraumes mit den geforderten konstanten hydrologischen Verhältnissen an den anderen Pegeln oberhalb Glückstadts nicht zu einem durch die Wahl des Anfangszeitpunktes der Doppelsummenanalyse und die Feinjustierung der Unschärfe gesteuerten Zufallsprodukt wird, werden die Ergebnisse im Rahmen dieser Untersuchung durch eine alternative differenziertere Betrachtungsweise abgesichert.

Glättung der oberwassernormierten Differenzwasserstandsganglinien

Eine wesentlich anschaulichere und aussagekräftigere Analysegrundlage zur Bestimmung eines geeigneten Bezugszeitraumes zur Durchführung der Regressionsanalysen bietet bei den hier vorliegenden Verhältnissen ein direkter Vergleich der Ganglinien zwischen den Scheitelwasserständen am jeweiligen Revierpegel und dem Referenzpegel Helgoland, wenn die Ganglinien der betrachteten Pegel durch eine übergreifende (oder auch gleitende) gewichtete Mittelwertbildung zuvor geglättet werden.

Bei der gewichteten Mittelwertbildung einer Zeitreihe werden die dem zu berechnenden Wert zeitlich benachbarten Werte mit immer geringerer Gewichtung berücksichtigt, je weiter sie vom aktuell zu mittelnden Wert entfernt sind. Gegenüber einer gleichgewichteten Mittelwertbildung können so insbesondere bei oszillierenden Zeitreihen langperiodische Schwingungen deutlicher sichtbar gemacht werden. Wenn die mittleren Wasserstände dabei noch um den Einfluss des Oberwasserabflusses bereinigt werden, kann so auch die relative Entwicklung der Wasserstände an den Pegelstandorten oberhalb Kollmars in die Untersuchungen zur Festlegung eines geeigneten Bezugszeitraumes einbezogen werden.

Anzumerken sei an dieser Stelle, dass grundsätzlich auch die Wasserstandsentwicklung an den Pegelnstandorten oberhalb Kollmars einer vergleichenden Betrachtung unterzogen werden kann, sei es durch eine Doppelsummenanalyse (vgl. a. Pegel Schulau in Abb. A.5.1-1) oder mit dem hier aufgezeigten Verfahren, wenn der Oberwassereinfluss für diese Pegel herausgerechnet wird. Für die hier verfolgten Zwecke reicht dazu auch die Verwendung eines linearen Ansatzes zu Beschreibung der örtlich veränderlichen Beziehung zwischen der Scheitelwasserstandsdifferenz und dem Oberwasserabfluss aus. Einen Vergleich mit der nichtlinearen Beziehung, wie sie aus der späteren Regressionsanalyse resultiert, zeigt Abb. A.5.1-2.

Abb.A.5.1-2: Vergleich unterschiedlicher Näherungsfunktionen zur Beschreibung des Oberwassereinflusses auf die Scheitelwasserstände (Ordinate º MTnw_RP - a_RP MTnw_HEL - b_RP MThb_HEL- e = ce = c × Q^d )

Zusammenfassung charakteristischer Abschnitte der Tideelbe

Die auf diese Weise geglätteten und oberwassernormierten Ganglinien der MTnw -Scheitelwasserstände sind mit Ihren Differenzen zur adäquaten Ganglinie am Referenzpegel Helgoland in den Abb. A.5.1-3 bis 6 dargestellt.

Aus Gründen der besseren Übersichtlichkeit wurden die Ganglinien der insgesamt 20 betrachteten Pegel dabei in vier charakteristischen Abschnitten der Tideelbe zusammengefasst. Unter dem Gesichtspunkt, dass die im weiteren Verlauf dieser Untersuchungen noch darzustellenden Ergebnisse nur exemplarisch und nicht für alle 20 untersuchten Revierpegel abgebildet werden können, zielt ein Aspekt dieser Zusammenfassung auch auf die Übertragbarkeit der noch folgenden Aussagen und beispielhaften Darstellungen von einem beliebigen Pegel eines charakteristischen Bereichs auf jeden anderen des gleichen Bereichs ab.

Dabei darf die nach den im Folgenden definierten Kriterien vorgenommene Abgrenzung keineswegs als absolut starre Festlegung betrachtet werden. Vielmehr kann von einem allmählichen Übergang ausgegangen werden, so dass die weiteren Aussagen bzgl. eines explizit genannten Bereiches natürlich immer auch in den Grenzregionen der Nachbarbereiche Gültigkeit besitzen.

Die Charakterisierung dieser vier Bereiche zeichnet sich hinsichtlich der oberwasserabflussbereinigten Tideniedrigscheitelwasserstände (MTnw[Q₀]) durch die jeweils über den Diagrammen definierten gemeinsame Eigenschaften aus:

Die auf diese Weise geglätteten und oberwassernormierten Ganglinien der MTnw -Scheitelwasserstände sind mit Ihren Differenzen zur adäquaten Ganglinie am Referenzpegel Helgoland in den Abb. A.5.1-3 bis 6 dargestellt.

Aus Gründen der besseren Übersichtlichkeit wurden die Ganglinien der insgesamt 20 betrachteten Pegel dabei in vier charakteristischen Abschnitten der Tideelbe zusammengefasst. Unter dem Gesichtspunkt, dass die im weiteren Verlauf dieser Untersuchungen noch darzustellenden Ergebnisse nur exemplarisch und nicht für alle 20 untersuchten Revierpegel abgebildet werden können, zielt ein Aspekt dieser Zusammenfassung auch auf die Übertragbarkeit der noch folgenden Aussagen und beispielhaften Darstellungen von einem beliebigen Pegel eines charakteristischen Bereichs auf jeden anderen des gleichen Bereichs ab.

Dabei darf die nach den im Folgenden definierten Kriterien vorgenommene Abgrenzung keineswegs als absolut starre Festlegung betrachtet werden. Vielmehr kann von einem allmählichen Übergang ausgegangen werden, so dass die weiteren Aussagen bzgl. eines explizit genannten Bereiches natürlich immer auch in den Grenzregionen der Nachbarbereiche Gültigkeit besitzen.

Die Charakterisierung dieser vier Bereiche zeichnet sich hinsichtlich der oberwasserabflussbereinigten Tideniedrigscheitelwasserstände (MTnw[Q₀]) durch die jeweils über den Diagrammen definierten gemeinsame Eigenschaften aus:

Bereich I : Revierpegel von Gr. Vogelsand bis Glückstadt (untere Tideelbe)

• kein spürbarer Oberwassereinfluss auf die MTnw-Scheitel,
• MTnw(Q0) £ MTnw Helgoland, stromaufwärts ansteigend,
• leicht fallende Tendenz gegenüber Helgoland (~ 0,25 cm/a)

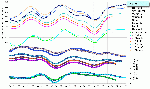
Abb.A.5.1-3: Entwicklung der MTnw-Scheitel im unteren Bereich der Tideelbe (charakteristischer Bereich I)

Bereich II : Revierpegel von Glückstadt bis Schulau (mittlere Tideelbe)

• schwacher bis mäßiger Oberwassereinfluss auf die MTnw-Scheitel,
• MTnw(Q0) £ MTnw Helgoland, stromaufwärts fallend,
• mäßig fallende Tendenz gegenüber Helgoland (0,3 - 0,65 cm/a).

Abb.A.5.1-4: Entwicklung der MTnw-Scheitel im mittleren Bereich der Tideelbe (charakteristischer Bereich II)

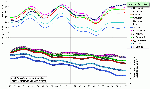
Bereich III: Revierpegel von Bunthaus bis Geesthacht (obere Tideelbe)

• signifikanter Oberwassereinfluss auf die MTnw-Scheitel,
• MTnw(Q0) ³ MTnw Helgoland, stromaufwärts ansteigend,
• deutlich fallende Tendenz gegenüber Helgoland (1,6 - 2,5 cm/a).

Abb.A.5.1-5: Entwicklung der MTnw-Scheitel im oberen Bereich der Tideelbe (charakteristischer Bereich III)

Auch wenn die MTnw-Ganglinien der Revierpegel Blankenese und St. Pauli - vom Verlauf und Trend her gesehen - sowohl am Ende des Bereichs II als auch an den Anfang des Bereichs III einsortiert werden könnten, sind bei der Analyse der Wasserstandsverhältnisse insbesondere am Pegel St. Pauli so viele standortspezifische Besonderheiten mit potentiellen Auswirkungen auf die Ergebnisse zu berücksichtigen, dass eine Aussage für diese Pegel nicht unbedingt als repräsentativ für einen größeren Bereich über das Stromspaltungsgebiet hinaus gelten kann.

Für das Stromspaltungsgebiet der Elbe macht es daher Sinn den gesonderten Bereich HH zu definieren, auch wenn darin mit den Stationen Blankenese und St. Pauli derzeit nur zwei Pegel enthalten sind.

Bereich HH: Revierpegel Blankenese u. St. Pauli (Stromspaltungsgebiet der Elbe)

• mäßiger Oberwassereinfluss auf die MTnw-Scheitel,
• MTnw(Q0) << MTnw Helgoland
• deutlich fallende Tendenz gegenüber Helgoland (~ 1,3 cm/a).

Abb.A.5.1-6: Entwicklung der MTnw-Scheitel im Stromspaltungsgebiet der Elbe (charakteristischer Bereich HH)

Durch die gewichtete Glättung der MTnw-Monatsmittelwerte (hier über 5 Jahre) wird in den Abb. A.5.1-3 bis -6 die langperiodische Bewegung des Tidegeschehens in der Deutschen Bucht und im Elbeästuar auch visuell gut erkennbar. Das mittlere Niveau des Tideniedrigwassers am Pegel Helgoland pendelt dabei in einem Bereich von ± 10 cm um einen langsam steigenden Trend von ~ 0,05 cm/a (im Schnitt der letzten 50 Jahre). Die MTnw-Scheitel der Revierpegel im unteren und mittleren Bereich der Tideelbe korrespondieren sehr eng mit diesen durch meteorologische Einflüsse erklärbaren Schwankungen. Im oberen Bereich der Tideelbe treten diese langfristigen Schwingungen allerdings nur noch stark gedämpft auf und scheinen sich mit zunehmender Annäherung an das Wehr Geesthacht diametral zur Amplitude in Helgoland abzubilden.

Die Ganglinien der MTnw-Scheiteldifferenzen zwischen Helgoland und den Revierpegeln an der unteren Tideelbe bis einschl. Kollmar weisen auch langfristig betrachtet nur einen relativ schwach ausgeprägten negativen Trend auf. Bei genauerer Betrachtung fällt auf, dass dieser Trend z. T. durch das zuletzt wieder verstärkt ansteigende Niveau von ~ 0,35 cm/a der MTnw-Scheitel in Helgoland bedingt ist. Das heißt: hier fällt nicht das örtliche MTnw, sondern es steigt nur nicht so wie erwartet, in gleichem Maß wie das MTnw am Referenzpegel Helgoland.

Dagegen wird es vor allem für die Revierpegel oberhalb Kollmars schwierig einen Zeitraum mit annähernd konstanten hydrologischen Verhältnissen zu definieren. Gegenüber dem Referenzpegel Helgoland sind hier die oberwasserabflussnormierten MTnw-Scheitel mit einem stetig fallenden Trend behaftet (im Maximum von bis zu 2,5cm/anno am Revierpegel Geesthacht). Eine zu Beginn der '90er zu beobachtende Stabilisierung der Verhältnisse, die teilweise sogar zu einer Umkehr des Trends zu führen schien, konnte sich langfristig nicht durchsetzten und fällt seit etwa 1996 wieder in den alten Trend zurück.

Empfindlichkeit der Regressionskoeffizienten gegenüber dem Bezugszeitraum

Um die Auswirkungen dieser beobachteten Trends auf die Qualität der durchzuführenden Berechnung genauer eingrenzen zu können und die Auswahl des zugrundegelegten Bezugszeitraumes zusätzlich abzusichern, wurden für alle 20 Revierpegel zunächst Regressionsanalysen über unterschiedlich lange Zeiträume in den '90er Jahren durchgeführt, die so nah wie möglich an den Zeitpunkt des zu beurteilenden Eingriffs heranreichten.

In Abb. A.5.1-7  sind exemplarisch die Koeffizienten a_RP und b_RP, die in dem der Regressionsanalyse zugrunde liegendem Modell zur Gewichtung des MTnw bzw. MThb am unabhängigen Referenzpegel Helgoland dienen, über die Stromkilometrierung von Gr. Vogelsand bis hin zum Wehr Geesthacht aufgetragen.

Abb.A.5.1-7: Entwicklung der resultierenden Regressionskoeffizienten a_RP und b_RP zur Gewichtung des MThw_HEL bzw. MThb_HEL entlang des Tideästuars für unterschiedlich lange Regressionszeiträume

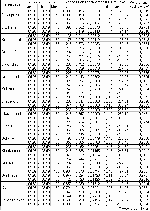
Die resultierenden Regressionskoeffizienten a_RP - e_RP und der Korrelationskoeffizient (R²) sind exemplarisch für 3 von insgesamt 6 untersuchten unterschiedlich langen Bezugszeiträumen in Tab. A.5.1-1 und -2 jeweils für das MTnw und MThw dargestellt.

Tab.A.5.1-1: Ergebnisse der Regressionsanalyse zur Korrelation der MTnw-Scheitel exemplarisch für 3 unterschiedliche, der Regression zu Grunde liegende, Zeiträume

Tab.A.5.1-2: Ergebnisse der Regressionsanalyse zur Korrelation der MThw-Scheitel exemplarisch für 3 unterschiedliche, der Regression zu Grunde liegende, Zeiträume

Die resultierenden Regressionskoeffizienten wurden im Rahmen einer Parameterstudie hinsichtlich ihrer Empfindlichkeit gegenüber dem gewählten Zeitraum und den damit verbundenen unterschiedlich stark ausgeprägten Tendenzen innerhalb dieser Phasen verglichen und bewertet. Als Ergebnis dieser Untersuchungen, konnten folgende Erkenntnisse für die Auswahl eines repräsentativen Zeitraumes für die Regressionsanalyse bei Verwendung von Monatsmittelwerten gewonnen werden:

• der zu berücksichtigende Zeitraum sollte mindestens 5 Jahre betragen, bei kürzeren Zeiträumen brechen die resultierenden Koeffizienten aus der ansonsten recht engbandigen Streuung aus (vgl. Abb. A.5.1-7),
• der Zeitraum sollte einen kompletten Jahreszyklus beinhalten, gerade bei kürzeren Zeiträumen spielt die ansonsten vorhandene Ungleichgewichtung von saisonalen Effekten eine nicht zu vernachlässigende Rolle,
• die insbesondere im Bereich der unteren Tideelbe zum Ende der 80-Jahre zu beobachtende deutliche Delle im Gang der relativen MTnw-Scheitel sollte nicht in dem zu berücksichtigenden Zeitintervall enthalten sein.
• Das Ende des zu berücksichtigten Zeitraumes sollte so nah wie möglich an den Zeitpunkt des zu beurteilenden Eingriffs heranreichen, um zu vermeiden, dass Ereignisse welcher Art auch immer, die zwischen dem Regressionszeitraum und dem Eingriff gelegen sind, das Ergebnis verfälschen.
• das Ende des zu berücksichtigten Zeitraumes kann ohne Auswirkungen auf die resultierenden Koeffizienten bis einschließlich Aug. '99 gewählt werden, erst danach werden die erwarteten Auswirkungen des Eingriffs deutlich sichtbar,
• die Wahl des Zeitraumes hat insbesondere im oberen Stromgebiet bei den MTnw-Scheiteln signifikante Auswirkungen auf die Größe der Konstanten (e).

Der letzte Spiegelpunkt ist für die weitere Auswertung insofern von Bedeutung, als dass in dem von Niemeyer gewählten Ansatz ein über die Zeit integrierter mittlerer Zustand beschrieben wird, der die gefundene empirisch funktionale Beziehung zwischen den berücksichtigten Einflussgrößen und dem lokalen Scheitelwasserstand genaugenommen auf einen Zeitpunkt, der etwa in der Mitte des der Regressionsanalyse zu Grunde liegenden Zeitraums liegt, reduziert. Ein über die Zeit veränderlicher Trend kann durch den von Niemeyer gewählten Ansatz ohne eine zeitabhängige Variable nicht abgebildet werden.

Diese Einschränkung darf bei einer späteren Beurteilung der zu ermittelnden Rechenwerte zur Bestimmung der ausbaubedingten Änderungen nicht außer Acht gelassen werden, wenn man die im Folgenden dargestellten resultierenden Auswirkungen eines solchen Trends auf die miteinander zu vergleichenden Mittelwerte oder mittleren Niveaus der Scheitelwasserstände vor und nach dem Ausbau betrachtet.

Einfluss einer trendbehafteten Ganglinie auf die Differenz von Mittelwerten

Die Folgen dieser Einschränkung, soll mit Abb. III1.1.1.1-8 am Beispiel der Ganglinie der MTnw-Scheitel am Revierpegel Bunthaus veranschaulicht werden. Hier werden die externen über die Zeit veränderlichen Einflussgrößen auf der rechten Seite der Gleichung (1) nach Beaufschlagung mit den Faktoren, wie sie aus der Regressionsanalyse resultieren, schrittweise von den beobachteten mittleren Scheitelwasserständen abgezogen. Auf der rechten Seite der Gleichung (1) verbleibt damit allein die Konstante (e) zur Beschreibung der nach der Subtraktion verbliebenen sog. Restdifferenz, die im untersten Diagramm als Ganglinie über die Zeit aufgetragen sind.

Bei entsprechender Auflösung der Ordinate (hier 5fach überhöht im Vergleich zu den absoluten Ganglinien) wird einerseits deutlich, dass sich die Streuung dieser Restdifferenzen in einem relativ engen Sektor von ±10 cm um die aus der Regressionsanalyse resultierende Konstante (e = -97,51) bewegen. Andererseits ist über die 10 Jahre betrachtet, auch ohne die lineare Ausgleichsgerade ein deutlicher Trend augenscheinlich, der wie bereits vorausgeschickt durch die Konstante (e) allein nicht abgebildet werden kann.

Vom Prinzip her ist das Ergebnis vergleichbar mit den Darstellungen der Abb. III1.1.1.1-3 bis -6). Dies ist auch nicht weiter bemerkenswert, wenn man berücksichtigt, dass schon dort von der Differenz der Scheitelwasserstände (hier: MTnw_PR - MTnw_HEL) bereits der Oberwassereinfluss abgezogen wurde. Im Vergleich dazu wird hier das MTnw_HEL noch mit dem aus der Regressionsanalyse resultierenden Regressionskoeffizienten (a_RP) gewichtet und zusätzlich das mit dem Regressionskoeffizienten (b_RP) gewichtete MThb_HEL in Abzug gebracht.

Abb. III 1.1.1.1-8  macht auch deutlich, dass die Bedeutung des Tidenhubs am Referenzpegel Helgoland (MThb_HEL) für den MTnw-Scheitel am jeweiligen Revierpegel aufgrund der geringen Schwankungen, die durch die Beaufschlagung mit Regressionskoeffizienten (b_RP) in der Größenordnung von -0,2 bis +0,6 noch zusätzlich gedämpft werden, und des zumindest auf die letzten 10 Jahre bezogenen absolut konstanten Verlaufs der Ganglinie, im Vergleich zu den beiden anderen Einflussgrößen als eher untergeordnet bezeichnet werden darf.

Noch deutlicher gilt diese Aussage übrigens für den Einfluss des Tidenhubs am Referenzpegel Helgoland (MThb_HEL) auf die mittleren Tidehochwasserscheitel im Regime, wenn man hier die Wirkung der resultierenden Regressionskoeffizienten (b_RP) von durchschnittlich 0,2 (vgl. Tab. A.5.1-2) berücksichtigt.

Abb.A.5.1-8:Subtraktion der externen Einflussgrößen von der Ganglinie der MTnw-Scheitel eines Revierpegels.

Obwohl oder gerade weil der schon in den Abb. III1.1.1.1-3 bis -6 in allen charakteristischen Abschnitten der Tideelbe beobachtete Trend einer langfristigen stetigen Abnahme der relativen MTnw-Scheitel nicht durch das anzuwendende Modell berücksichtigt werden kann, übt er dennoch über den der Regressionsanalyse zu Grunde gelegten Bezugszeitraum einen aus statistischer Sicht unerwünschten Einfluss auf die resultierenden Regressionskoeffizienten aus.

Welche Auswirkung diese Tatsache hinsichtlich der Auswertung der ausbaubedingten Änderungen der mittleren Scheitelwasserstände zur Folge haben kann, wird im Folgenden wiederum am Beispiel der MTnw-Scheitel diesmal für den Revierpegel Blankenese dargestellt.

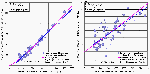
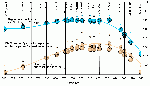
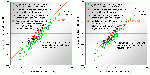
Dazu werden die unter Verwendung der resultierenden Regressionskoeffizienten berechneten Zielgrößen (hier: exemplarisch die MTnw-Scheitel für 2 unterschiedlich lange Bezugszeiträume am Revierpegel Blankenese) zunächst in einem Streudiagramm über die Eingangsdaten der Regressionsanalyse (hier: Monatsmittelwerte der gemessenen MTnw-Scheitel) aufgetragen (vgl. grüne Symbole in Abb. A.5.1-9).

Abb.A.5.1-9:Streudiagramm der gemessenen und berechneten MTnw-Scheitel am Revierpegel Blankenese sowie die Mittelwerte vor und nach dem betrachteten Eingriff.

Das Streudiagramm wird bei Regressionsrechungen häufig zur Visualisierung und Überprüfung der Güte des gewählten Modells verwendeten. Je näher die aufgetragenen Punkte an der Diagonalen f(x)=x liegen desto geringer ist die Abweichung zwischen den berechneten und gemessenen Werten. Der angegebene Korrelationskoeffizient R², der sonst eigentlich nur ein Maß für die Bestimmtheit eines funktionalen Zusammenhangs ist, kann bei dieser Art der Auftragung auch als Maßzahl für die Größe der Streuung herangezogen werden (R² kann maximal den Wert 1 annehmen, dazu müssten alle Punkte exakt auf der Diagonalen liegen).

Vergleicht man die hier angegebenen Korrelationskoeffizienten mit denen der anderen Stationen in Tab. A.5.1-1, so liegt das gewählte Beispiel eher am hinteren Ende. Inwieweit sich weitere unabhängige Einflussgrößen wie die lokalen Windfelder über dem Elbeästuar parametrisieren lassen und sich eine Berücksichtigung solcher zusätzlichen kausalen Wirkparameter positiv auf die Güte der Streuung auswirkt, wird in einer noch laufenden Studie untersucht.

An dieser Stelle soll das Streudiagramm aber auch gar nicht dazu dienen, über die Güte der Streuung zu diskutierten oder gar den eigentlich nicht anders erwarteten funktionalen Zusammenhang zwischen den verwendeten unabhängigen Eingangsvariablen und der abhängigen Zielgröße zu verifizieren, sondern das Augenmerk auf die ergänzende Eintragung der Ereignisse nach dem Eingriff bzw. Prognosezeitraum (rote Symbole) lenken. Diese setzen sich an dem hier gewählten Pegelstandort nämlich deutlich sichtbar von den in grüner Farbe dargestellten Ereignissen vor dem Eingriff nach oben ab. Im Mittel liegen diese Ereignisse um 12,8 cm im Beispiel mit dem längeren Bezugszeitraum links bzw. um 10,3 cm im Beispiel mit dem kürzeren Bezugszeitraum rechts oberhalb der Diagonalen. Eine Erklärung für die Ursache der unterschiedlich großen Differenz wird am Ende dieser Betrachtung noch nachgeliefert.

Die Darstellung belegt zunächst einmal, dass die Ereignisse für den Prognosezeitraum durch das auf den Bezugszeitraum vor dem Eingriff kalibrierte statistische Modell höher berechnet werden, als sie in dieser Zeit tatsächlich gemessenen wurden. Im Umkehrschluss hieße dies, bei Anwendung des dem NIEMEYER-Verfahren zu Grunde liegenden theoretischen Gedankenmodells, dass die beobachteten Wasserstände gegenüber dem hypothetischen Niveau, das ohne den Eingriff zu erwarten gewesen wäre, ausbaubedingt gefallen sind.

Vom Grundsatz her, ist gegen diese Aussage nichts einzuwenden, schließlich war ein ausbaubedingtes Absinken der MTnw-Scheitel auch in der UVU durch die Untersuchungen im HN-Modell der BAW prognostiziert worden (vgl. Abb. III.1.1.1-1). Wenn die zuvor genannten Voraussetzungen zur Anwendung des Verfahrens, nämlich konstante Verhältnisse über die gesamte Dauer des Bezugszeitraumes vor dem Eingriff erfüllt wären, könnte man bei dem gedanklichen Modell auch den nächsten Schritt mitgehen und die nun beobachtete Differenz als Ausbaufolge quantifizieren.

Allein die zuvor aufgezeigte Tatsache, dass diese konstanten Verhältnisse genau genommen an fast keinem Pegelstandort gegeben waren, impliziert in die auf diese Weise abgetragene Differenz der Mittelwerte durch die Ausblendung der zeitlichen Dimension eine darstellungsbedingte Fehlinterpretation von Ursache und Wirkung. Die Differenz der Mittelwerte im Prognosezeitraum in voller Höhe allein den Ausbaufolgen zuzuschreiben wird den hier vorliegenden trendbehafteten Verhältnissen unter Berücksichtigung der Limitierung des verwendeten Modells in keiner Weise gerecht.

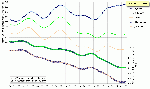
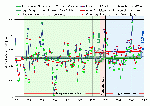
Um diese Feststellung besser zu veranschaulichen, wurden die gemessenen und berechneten Daten des rechten Streudiagramms jeweils auch als Ganglinie über die Zeit aufgetragen (vgl. Abb. A.5.1-10). Ergänzt wird die Darstellung zum einen durch die für den Regressions- und Prognosezeitraum jeweils resultierenden statischen Mittelwerte der gemessenen und berechneten Daten sowie den beiden Trendlinien, denen hier die gewichteten Mittelwerte über ein gleitendes Fenster von 3 Jahren zu Grunde liegen. Letztere sind für diese Darstellung über den gesamten betrachteten Zeitraum sowohl vor als auch während und nach dem zu bewertenden Eingriff durchgehend berechnet.

Abb.A.5.1-10: Vergleich der gemessenen und berechneten Ganglinien der MTnw-Scheitel am Revierpegel Blankenese.

Dass die statischen Mittelwerte der gemessenen und berechneten Daten im Regressionszeitraum identisch sind, ist durch das Prinzip der Minimierung der Summe der Fehlerquadrate bedingt, auf dem das Wesen jeder Regressionsanalyse basiert und muss so sein. Dass dieses Niveau allerdings nahezu identisch ist mit dem Niveau des Mittelwertes der gemessenen Daten im Prognosezeitraum ist reiner Zufall und wird sich mit der Anzahl der jeweils vor bzw. nach dem Eingriff berücksichtigten Ereignisse verschieben.

Dennoch ist dieser Zufall insofern eine nicht zu erwartende Besonderheit als er einem lokalen Beobachter den subjektiven Eindruck vermitteln könnte, dass das MTnw in den bisherigen 3 Jahren nach dem zu bewertenden Ausbau der Fahrrinne im Mittel gar nicht wie prognostiziert gegenüber dem Bezugszeitraum gefallen ist.

Hier muss allerdings entgegnet werden, dass in den vorliegenden ersten drei Jahren des Prognosezeitraumes der am Referenzpegel Helgoland beobachtete leichte Anstieg des MThw in Verbindung mit einem relativ hohen Oberwasserabfluss (vgl. a. Kap. III.1.1.3.1) eigentlich auch zu einer Erhöhung des örtlichen MTnw am Revierpegel Blankenese hätte führen müssen, wie es hier durch den Verlauf der Trendlinie für die berechneten Werte auch sehr schön angezeigt wird.

Das eigentliche Augenmerk sollte bei der Abb. A.5.1-10 aber auf den Verlauf der Trendlinien im der Regression zu Grunde gelegten Bezugszeitraum gerichtet werden. Dort zeigen die Trendlinien an, dass die gemessenen Werte (grüne Symbole/ Trendlinie) in der ersten Hälfte des Regressionszeitraumes durch die Modellrechnung (rote Symbole/ Trendlinie) eher unterschätzt werden, während sie in der zweiten Hälfte in gleichem Maße überschätzt werden. Ausschließlich in der Mitte, wo sich die beiden Trendlinien schneiden, ist also die Differenz zwischen den berechneten gemessenen Werten gleich Null.

Bei der Regressionsanalyse über eine trendbehaftete Ganglinie stellen sich die Regressionskoeffizienten so ein, dass sich die verbleibenden Differenzen = Fehler zur Minimierung der Summe der Fehlerquadrate gleichmäßig nach links und rechts verteilen müssen, was einleuchtet, wenn man bedenkt, dass zwei mal das Quadrat des halben Fehlers schließlich kleiner ist als das Quadrat des ganzen Fehlers. Die Differenzen die es in diesem Fall zu verteilen galt, resultieren im Wesentlichen aus dem in den Abb. III1.1.1.1-3 bis -6  bereits aufgezeigten negativen Trend der MTnw-Scheitel, der nach stromauf zunehmend deutlicher ausgeprägt erscheint. Wie bereits in der Diskussion zur Abb. III1.1.1.1-8  dargelegt, kann dieser Trend durch das hier verwendete Modell nicht abgebildet werden.

Dies hat zur Folge, dass der Vergleich zwischen den Ergebnissen der Modellrechnung und der Messung bereits am Ende des Regressionszeitraumes, also noch bevor der zu bewertende Eingriff vorgenommen wurde, mit einer Fehlerdifferenz behaftet ist, die im Folgenden als Anfangsfehler bezeichnet werden soll. Dieser Anfangsfehler, der im vorliegenden Beispiel immerhin rd. 5 cm beträgt, wird bei einem Vergleich der statischen Mittelwerte der Modellrechnung und der Messungen nicht berücksichtigt. Dies wäre ja auch nicht nötig, wenn die vorausgesetzten konstanten Verhältnisse über den gesamten Bezugszeitraum vorgelegen hätten.

Die Modellrechnungen zur Prognose der Werte, die ohne den Eingriff zu erwarten gewesen wären, basieren also auf einem gewissermaßen statischen Zustand, der die mittleren Verhältnisse während des der Regression zu Grunde gelegten Zeitraumes repräsentiert und damit die Variationen der berücksichtigten unabhängigen Einflussgrößen auch lediglich dem mittleren Niveau dieses Zeitraumes hinzufügen kann. Verlief der Trend in diesem Zeitraum auch nur einigermaßen stetig, so kann das mittlere Niveau etwa zur Halbzeit des Regressionszeitraumes angesiedelt werden, was im vorliegenden Beispiel ca. Ende 1996 heißt. Bei der ausschließlichen Betrachtung der Mittelwerte würde also der Zustand nach dem Eingriff mit dem Zustand von 1996 verglichen und die Differenz als Ausbaufolge quantifiziert. Dass diese Vorgehensweise die tatsächlich dem Eingriff zuzuordnende Veränderung überschätzt, muss also - wie bereits eingangs betont - bei der Bewertung der Rechenwerte berücksichtigt werden.

Nun wird auch die Zunahme der Mittelwertdifferenz bei dem längeren Regressionszeitraum in Abb. III1.1.1.1-9 verständlich. Vorausgesetzt dass der Trend über den gesamten Zeitraum einigermaßen stetig verlief, basiert die Modellrechnung für den längeren Prognosezeitraum in diesem Beispiel auf einem mittleren Niveau, das gegen Ende 1994, also zwei Jahre früher und damit geringfügig höher angesiedelt werden kann.

Die Ausführungen bis hierher haben gezeigt, dass eine eindeutige ursächliche Zuordnung der Mittelwertdifferenz zwischen Modellrechnung und Beobachtung nicht so ohne Weiteres möglich ist, wenn an dem zu untersuchenden Pegelstandort im Regime vor dem Eingriff keine konstanten Verhältnisse vorgefunden werden können.

Um trotz dieser Einschränkungen dennoch eine Aussage über die Größe der wohl allein dem Eingriff zuzuordnenden Änderungen der mittleren Tidescheitelwasserstände machen zu können, müssen die verfahrensbedingten, weil vom Modell nicht abzubildenden Differenzen eliminiert werden.

Im Rahmen dieser Auswertung werden die in der UVU prognostizierten ausbaubedingten Änderungen der Scheitelwasserstände im Prognosezeitraum daher als Parallele zum zuletzt beobachteten Trend abgesetzt und ein Überschreiten dieser Schwellenwerte durch die als gleitende Mittelwerte aufgetragenen Differenzen zwischen der Modellrechnung und Beobachtung zunächst lediglich einer visuellen Überprüfung und Bewertung unterzogen (vgl. Kap. III.1.1.1.1).

nach oben